Approximating the 1D wave equation using Physics Informed Neural Networks (PINNs)
PhD Student at FAU MoD – Research Center for Mathematics of Data under the “Women in Mathematics of Data” program
September 2022
• See the complete report by Dania Sana
Introduction
Accurate and fast predictions of numerical solutions are of significant interest in many areas of science and industry. On one hand, most theoretical methods used in the industry are the result of deriving differential equations that are based on conservation laws, physical principles, and/or phenomenological behaviors for a particular process. On the other hand, real-time capable methods and algorithms are required in modern industrial applications. In the view of this, very recently, Physics-Informed Neural Networks (PINNs) architec- tures, which combine the real data and the partial differential models (PDEs) together with a respective set of boundary and initial conditions, have started to arise frequently in many areas of science and engineering (see [17], [4], [2] and [9]) and emerged as a powerful tool for developing flexible PDE solvers (see NVIDIA [12] and DeepXDE toolbox [5]).
While the focus of other methods employing neural networks for solving PDEs is on mitigating the curse of dimensionality in high dimensions, the strength of PINNs lies in their flexibility in that they can be applied to a great variety of challenging PDEs, whereas classical numerical approximations typically require tailoring to the specifics of a particular PDE. e.g., strong nonlinearities, convection dominance or shocks.
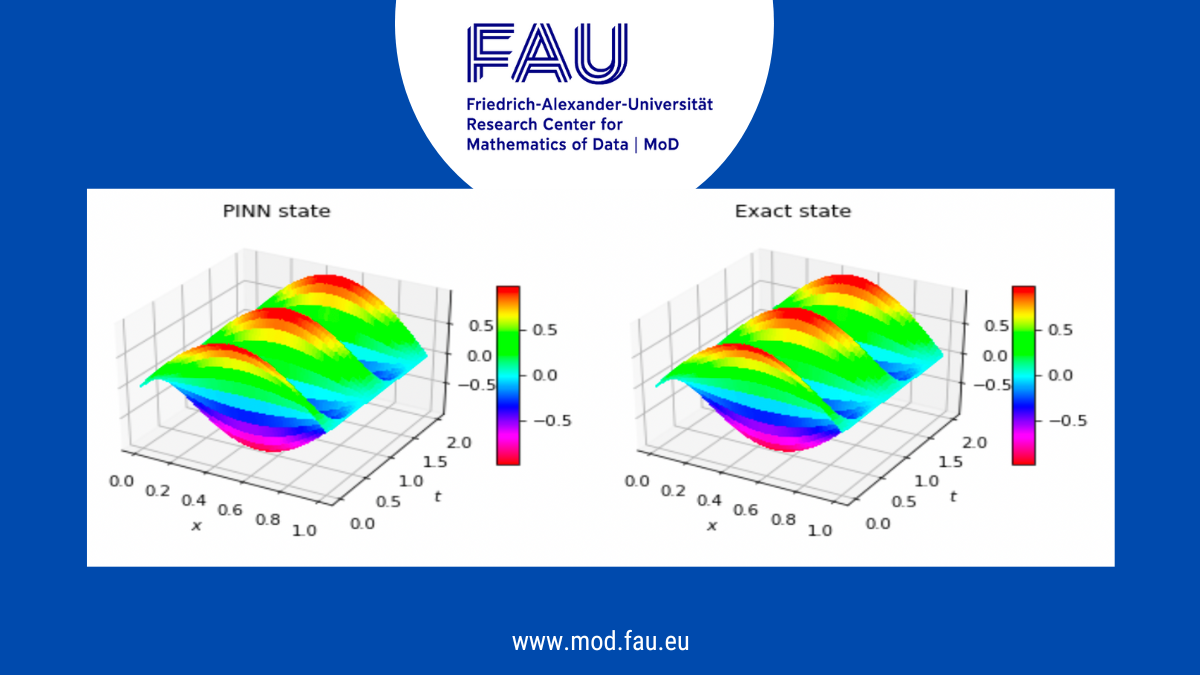
The intrinsic Machine-Learning (ML) nature of PINNs enables huge speed-ups for simulations at infer- ence time (i.e., after training) while the introduced physics ensures the conservation of the physical laws behind the problem. For the sake of simplicity, we take the wave equation as a basic model, the behavior of solution is well understood in theoretically and practically. Moreover, we mainly focus on revisiting the classical PINNs framework for solving forward and inverse problems, and on generating a solver in Python (see in our open-source on GitHub)
Abstract
This report summarizes the research activities and results obtained during the internship in the Research Center for Mathematics of Data in Erlangen. We present our progress on the application of Physics-Informed Neural Networks (PINNs) to solve various forward and inverse problems in PDEs, where we take the well- understood 1 dimensional wave equation as an example for numerical experiment and error analysis.
For forward problems (computing numerical solutions of given systems), we first establish a general framework of PINNs- that are trained using the loss functions to respect the governing physic laws and match the initial and boundary conditions. This model is able to solve the forward initial boundary valued problem (IBVP), and has shown promising numerical results in different cases even in the extreme case of no data. The requirement of accurate and fast prediction of numerical solutions is studied in two approaches: 1) Analyzing and evaluating the performance of the PINNs model by comparing its output to the analysis solution and examining the training and validation error; 2) in parallel, we review various structure and size of NN (number of nodes and layers) and investigate the required computational time, in order to achieve a satisfying performance of our model. More complicated cases, e.g. mixed boundary conditions, or degenerating wave equations, can be solved in the same framework.
For inverse problems, we generalize the PINNs algorithm to calculate the boundary control to realize the null controllability of the system in a given finite time. Additionally, we combine the model-driven and data-driven approach in solving the parameter identification problem.
This proposed PINNs methodology is an elegant and flexible way to include physical knowledge in machine-learning algorithms and accelerate the approximation and accuracy when real data are used. The results and numerical experiments presented in this report should lead to not only a deep theoretical understanding (e.g. convergency and accuracy study) in the future, but also to a practical usage of PINNs framework to solve both forward and inverse physical problems from real world applications.
Keywords: physics-informed neural networks, machine learning, wave equation, boundary controllability, parameter identification
An implementation of Physics-Informed Neural Networks (PINNs) to solve various forward and inverse problems for the 1 dimensional wave equation.
Wave_equation.py solves the 1d wave equation
Wave_equation_otherBC solves the 1d wave equation with Neumann boundary conditions
test_loss_time.py shows the test error-computational time dependency for a specific structure of neural network
train_error_val_error_time.py displays the train error/validation error/computational time-size of training set dependencies
all_together_loss_time.py shows the test error-computational time dependency for different structures of neural networks.
changing_nodes_test_loss.py shows the test error-computational time dependency for neural network structures with different numbers of nodes.
inverse_problem.py solves the inverse problem of the 1d wave equation
first_case_no_damage.py solves the degenerating 1d wave equation when a(x)=4
second_case_damage.py solves the degenerating 1d wave equation when a(x)=8|x−0.5|
third_case_double_damage.py solves the degenerating 1d wave equation when a(x)=16|x−0.5|^2
control.py solves the null controllability problem of the 1d wave equation.
degenerate_wave.m solves a wave equation u_tt(t,x)+a(x)u_xx(t,x)=0 on x∈(0,1) in which the stiffness is a(x)=4(2|x−\frac{1}{2}|)^\alpha by finite differences. (used for comparison)
• See the complete report by Dania Sana
Don’t miss out!
Internship program for female researchers – Women in Mathematics of Data